
It can be difficult to detect the underlying trend of a time series in the presence of anomalies, due to unwanted noise. Fortunately, there are techniques to take into account those anomalies, so you can work with this kind of time series. One of them is the moving median.
What is Robustness?
Implicit or explicit assumptions are often made in statistics. These might be about the distribution, the independence, the randomness or other characteristics of data. Those assumptions might not be always true, but often are “true enough.” For example, we can assume a time series to be normally distributed when in reality it is only almost normally distributed. We can then use this assumption to perform mathematical computations.
So what is robust statistics? It’s all about the “almost”. A non-robust statistical formula will yield results that make no sense when the assumption isn’t 100% true. Robust statistics, on the other hand, will produce results that make sense, perhaps with some small error, even though the assumption wasn’t 100% true. It also means that robust statistic should not be affected by outliers or anomalies.
In Robust Statistics 2nd Edition, Peter J. Hughes and Elvezio M. Ronchetti give this good definition about robust statistics:
“A minor error in the mathematical model should cause only a small error in the final conclusions.”

Moving Average Versus Moving Median
Moving averages are commonly used to smooth or remove the noise of a time series. It works well, but the presence of anomalies can affect the underlying trend calculation. Robust statistics shouldn’t be affected by outliers or anomalies. Let’s demonstrate how the moving median formula is a robust statistic.
First, using R language, we create an anomalous seasonal time series:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | createDay <- function(noise=0) { point=seq(0, pi, by=0.02) connection=sin(point) noise <- rnorm(length(point), 0, noise) return(connection+noise) } createDays <- function(totalDays, noise=0) { allDays <- c() for (day in 1:totalDays ) { allDays <- c(allDays, createDay(noise)) } return(allDays) } set.seed(10) days = createDays(3, 0.05) p1 <- days[0:270] p2 <- 2.5 # Anomaly here p3 <- days[(280+2):length(days)] strangeDay <- append(append(p1, p2), p3) plot(as.ts(strangeDay), ylim=c(0, 3), col="#e15f3f", lwd = 2) |
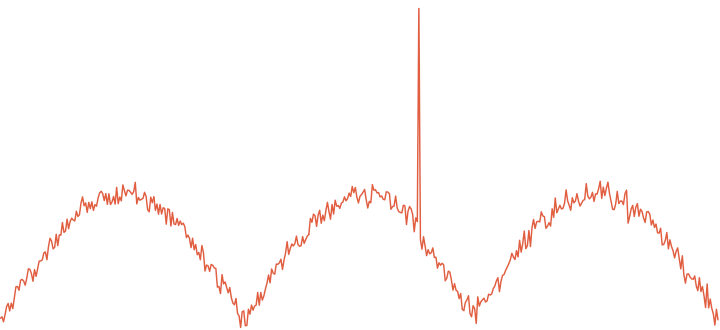
Raw time series with outliner
Moving Average Isn’t Robust
The commonly used moving average isn’t robust because it smoothes the anomaly, but doesn’t remove it. As a result, the outlier is “melted” into the size of the windows. In this example, the anomaly is allocated over 3 values.
1 2 3 4 5 6 7 | #install and import lib install.packages("forecast") library(forecast) movingAverage = ma(strangeDay, 3) plot(as.ts(movingAverage), ylim=c(0, 3), lwd = 2) |
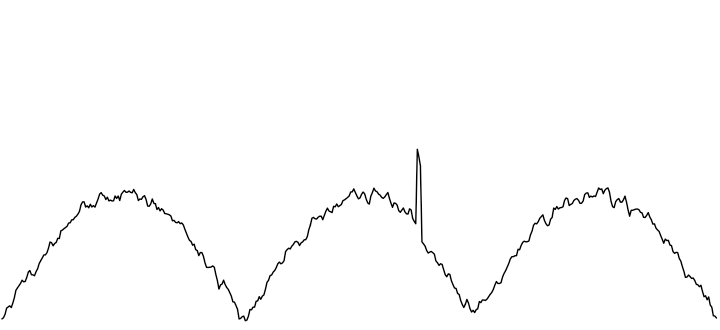
Moving average keeps the outlier
Moving Median Is Robust!
The moving median isn’t as popular as the moving average, but offers some interesting capabilities. The moving median provides a more robust estimate of the trend compare to the moving average. It isn’t affected by outliers: in fact, it removes them!
1 2 3 | movingMedian = runmed(strangeDay, 3) plot(as.ts(), ylim=c(0, 3), col="#27ccc0", lwd = 2) |
The moving median matches the definition of a robust statistic. “A minor error [the anomaly] in the mathematical model [the moving median] should cause only a small error in the final conclusions”.
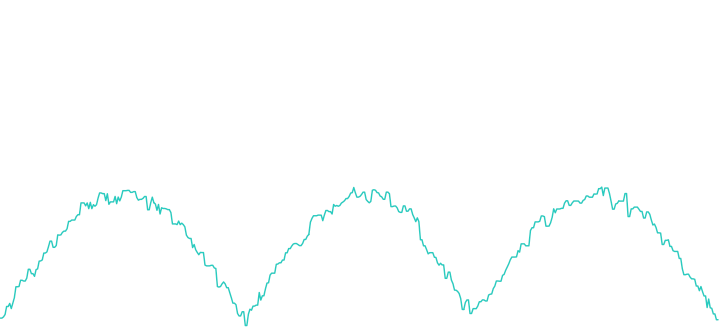
Moving median “removes” the outlier
Monitor & detect anomalies with Anomaly.io
SIGN UP

 sending...
sending...