
Previously, we looked at using Twitter Breakout (EDM) to detect Anomalies. As with the popular E-Divisive, EDM detects mean shift and changes in distribution. Both algorithms work with seasonal time series, but perform even better without seasonality.
Change Point Doesn’t Work (Well) with Seasonality
To demonstrate the “weakness” of change point, let’s generate some fake seasonal time series. Then we will try to detect anomalies using two different change point detection algorithms: EDM and E-Divisive.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | # install E-Divisive and EDM install.packages("Rcpp") install.packages("ecp") install.packages("devtools") devtools::install_github("twitter/BreakoutDetection") library(Rcpp) library(ecp) library(BreakoutDetection) createDay = function(noise=0) { point=seq(0, pi, by=0.02) connection=sin(point) noise = rnorm(length(point), sd = noise) return(connection+noise) } createDays = function(totalDays, noise=0) { allDays = c() for (day in 1:totalDays ) { allDays = c(allDays, createDay(noise)) } return(allDays) } set.seed(1234) p1 = createDays(3, 0.2) anomaly = createDays(1, 0)*2 + rnorm(158, sd = 0.07) days = c(p1, anomaly) plot(as.ts(days)) # EDM - fail res = breakout(days, min.size=158, method='multi', beta=.001, degree=1, plot=TRUE) res$plot # E-Divisive - fail ediv = e.divisive(as.matrix(days), min.size=158, alpha=1) plot(as.ts(days)) abline(v=ediv$estimates,col="blue") |
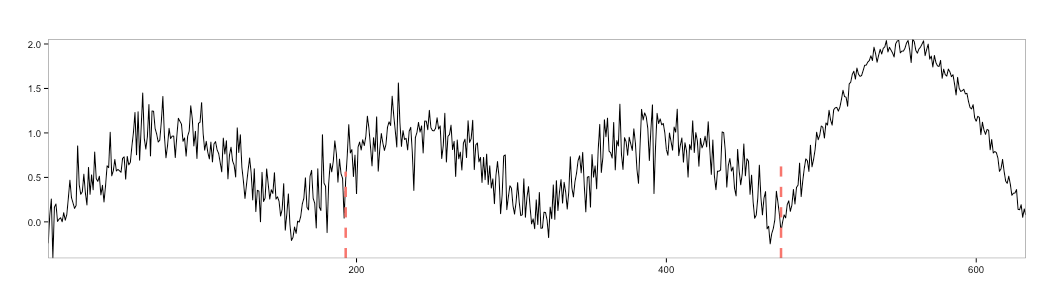
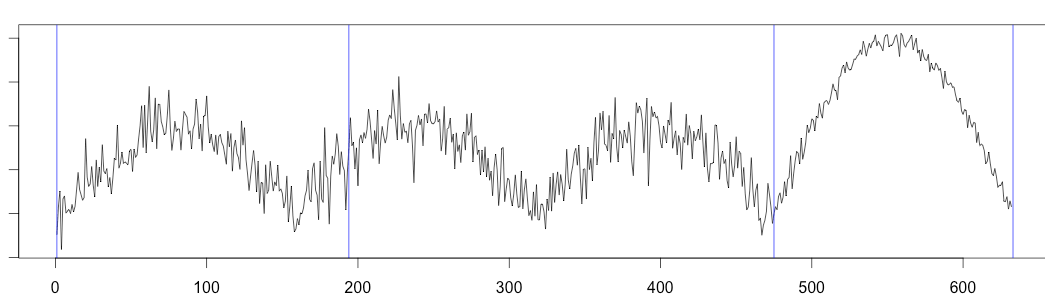
As we can see, due to the seasonality of the time series, traditional change point detection doesn’t work very well.
Removing the Seasonality
To use change point detection effectively, we need to remove the seasonality from our time series. And to do that, we need to know the period of the seasonality. In this case, we know the seasonality to be 158 data points per day. If we don’t know, it’s possible to calculate the seasonality using a Fourier Transform. We also need to know if the time series is multiplicative or additive. In our example, I have an additive time series, but most of the time it is multiplicative. With this information, we can now decompose to remove the seasonality. Finally, we can run the change point detection again to get a successful result.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | #remove seasonal decomposed_days = decompose(ts(days, frequency = 158), "additive") noSeasonal = days - decomposed_days$seasonal #remove seasonal decomposed_days = decompose(ts(p1, frequency = 158), "additive") noSeasonal = days - rep(decomposed_days$seasonal[0:158],4) # EDM - success res = breakout(noSeasonal, min.size=158, method='multi', beta=.001, degree=1, plot=TRUE) res$plot # E-Divisive - success ediv = e.divisive(as.matrix(noSeasonal), min.size=158, alpha=1) plot(as.ts(noSeasonal)) abline(v=ediv$estimates,col="blue") |
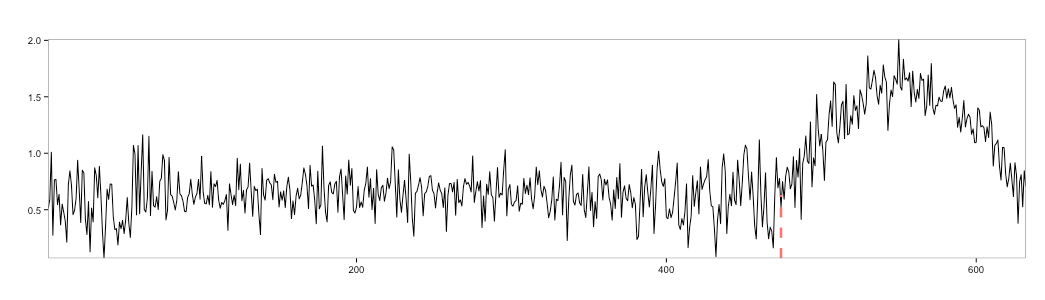
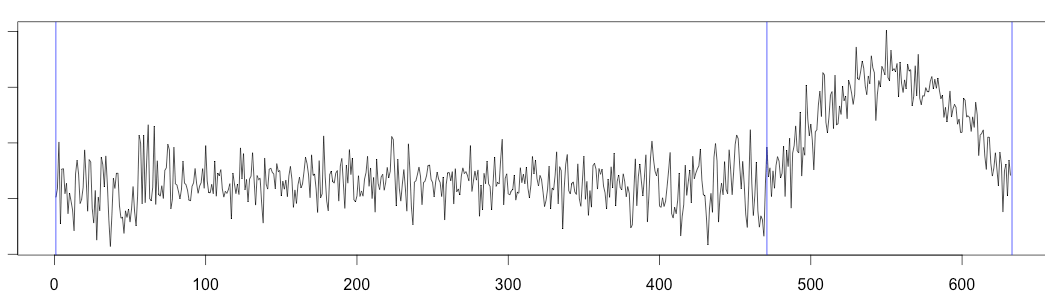
With the seasonality removed, breakout EDM and E-Divisive work a little bit better.
Monitor & detect anomalies with Anomaly.io
SIGN UP

 sending...
sending...